Nous allons voir d'abord les incertitudes qui pèsent sur la production des modèles numériques dans leur capacité à simuler le comportement de l'atmosphère. Puis nous verrons un peu la statistique des erreurs lorsque cela est transcrit en termes de temps qu'il fait, le temps concret auquel nous sommes sensibles.

Fiabilité de la modélisation numérique

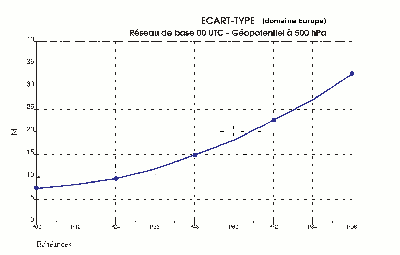Figure 5

Le risque d'un écart entre la simulation numérique et l'atmosphère réelle est d'autant plus grand que l'échéance est lointaine, il augmente même d'autant plus vite que l'échéance est lointaine. C'est ce que montre la figure 5. Le paramètre présenté sur cette figure mesure une « distance » entre la vraie topographie de la surface 500 hpa et celle prévue par le modèle (voir la figure 1 qui donne un exemple de carte de cette surface, représentative de la circulation atmosphérique vers 5500 m d'altitude). On peut constater que l'erreur augmente deux fois plus sur les jours J+3 et J+4 que sur J+1 et J+2. On comprend ainsi pourquoi la dégradation de fiabilité est très rapide lorsqu'on essaye de voir trop loin.

La dégradation n'est pas uniforme, ni dans le temps, ni dans l'espace. Il y a des situations plus prévisibles que d'autres. Par exemple, avec un bel anticyclone d'hiver, bien installé, on peut savoir que l'on a plusieurs jours de beau temps devant soi avant que les signes d'affaiblissement n'apparaissent. Et pour une situation donnée, l'atmosphère peut être plus stable, donc plus prévisible  dans certaines régions que d'autres. Nous allons illustrer cela avec les cartes de « spaghetti » de la Figure 6 (extraites de http://www.wetterzentrale.de/topkarten/fsenseur.html puis « 500hpa Geopot. Spaghetti »)

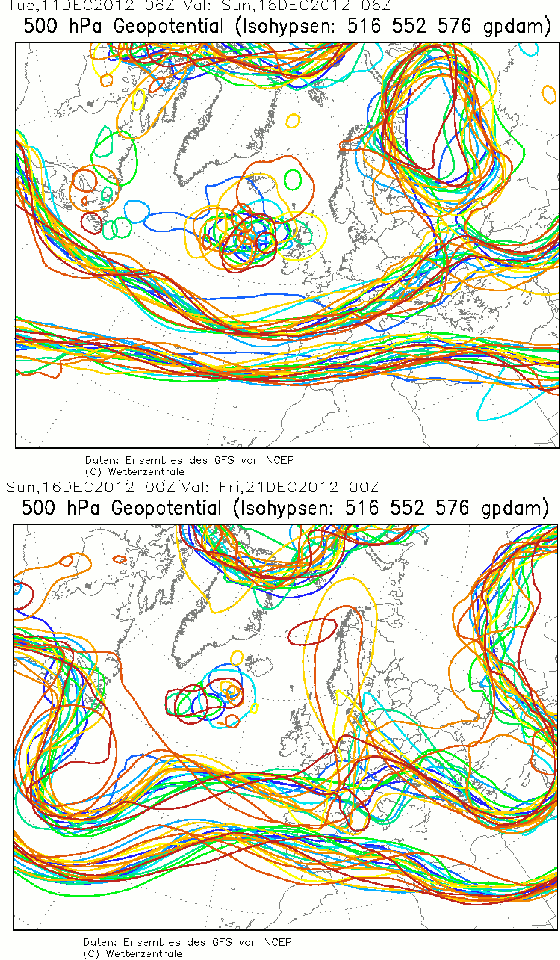
Figure 6

« Spaghetti » à 500 hpa, pour une échéance de 5 jours. En haut le 11/12/12 pour le 16/12 et en bas le 16/12 pour le 21/12.

Ces cartes sont dérivées du type de celle que montre la figure 1 : topographie de la surface fictive où la pression vaut 500 hpa. On n'a gardé que trois lignes de niveau (5160, 5520 et 5760 m), mais en les prenant dans vingt membres de l'ensemble de prévisions faites toutes le même jour en modifiant l'état initial, un peu différemment pour chacun des membres. Sur la carte du haut produite le 11 décembre pour le 16 on a affaire à une situation assez bien prévisible sur l'Europe car le fuseau des spaghetti y est compact. C'est nettement plus instable sur l'océan entre Irlande et Groenland. La carte du bas produite le 16 pour le 21 décembre, soit à la même échéance de cinq jours pour la prévision, montre au contraire une situation complètement imprévisible sur l'Europe. Les différentes prévisions de l'ensemble présentent des morphologies opposées. On ne sait si on sera sous un creux ou une bosse ce qui correspond à des types de temps radicalement différents, du pire au meilleur.

Il n'est pas mauvais de jeter un coup d’œil à ces cartes facilement accessibles sur Internet lorsque l'on consulte un bulletin de prévision pour plusieurs jours à l'avance. Cela donne très rapidement une idée graphique de la fiabilité de la rédaction qu'on a sous les yeux !

Pour terminer ce chapitre, un mot sur l'évolution au fil des années de la qualité de la production de prévision numérique.

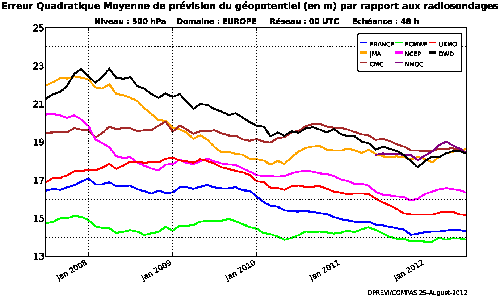Figure 7

Cette figure présente l'évolution de 2008 à 2013 du même paramètre que celui qui est présenté en Figure 5 (distance entre les valeurs prévues et la réalité pour l'altitude de la surface 500 hpa) pour la prévision deux jours à l'avance des principaux modèles du monde météorologique. Les courbes sont certes un peu chaotiques, mais la tendance est celle d'une amélioration continue. En moyenne, on gagne l'équivalent d'un jour d'échéance tous les dix ans (par exemple, la prévision à cinq jours a aujourd'hui la même qualité que la prévision à quatre  jours en 2003).

Notons au passage que si le graphique avait présenté les résultats pour la prévision à 24 heures au lieu de 48, il aurait été l'occasion d'un cocorico ! Le modèle français est très récemment devenu le meilleur à cette échéance, passant devant le modèle européen (ECMWF) ce qui n'était jamais arrivé. Pourvu que ça dure.

Statistiques des erreurs sur le temps concret

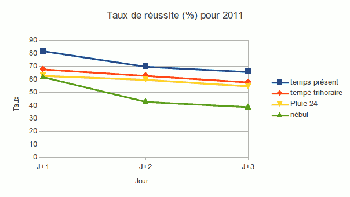 Figure 8

La figure 8 donne le taux de réussite sur les paramètres de la base de données quantifiées prévues à Météo-France. Il s'agit de valeurs ponctuelles calculées automatiquement mais expertisées par des spécialistes humains avant mise à disposition des utilisateurs.

Le « temps présent » c'est le temps qu'il fait (RAS=Rien A Signaler, précipitations ponctuelles ou généralisées, orages, brouillards ponctuels ou généralisés). « Pluie 24 » est la quantité tombée en 24 heures, ce qui est plus difficile à faire qu'un simple pluie – non pluie.

Le graphique montre la diminution de qualité de J+1 à J+3. Curieusement, la décroissance ne s'accélère pas avec l'échéance comme pour la production brute des modèles. Ceci indique peut-être que pour J+1 le prévisionniste humain est encore capable d'apporter une plus-value.

Les prévisions de données quantifiées ne sont pas produites au delà de J+3 car les risques de grosses inexactitudes sur la situation d'ensemble rendent un peu illusoire l'estimation ponctuelle de paramètres quantitatifs.

Aparté sur la signification de « taux de réussite » et des statistiques météorologiques

[ Cette section n'est pas nécessaire à la compréhension d'ensemble. Il suffit au lecteur pressé de la sauter ]

Le taux de réussite est le rapport du nombre de bonnes prévisions au nombre total de prévisions. C'est cette quantité qui est généralement utilisée par les producteurs de prévisions pour communiquer avec leur clients, tout simplement du fait de la simplicité de ce paramètre et de la facilité avec laquelle on peut dire ce qu'il représente.

Le taux de réussite est cependant une mesure très incomplète de la qualité des prévisions, et ce pour trois raisons : sa signification dépend de la climatologie du phénomène, une prévision au hasard peut avoir un taux de réussite élevé et enfin il ne dit rien sur les éventuels biais de la prévision.

Prenons l'exemple d'une prévision pluie – non pluie sur la journée. À Paris, pour une année normale on a 70 % de jours sans pluie et 30 % de jours avec pluie. Notons déjà que la « prévision » triviale qui consisterait  à annoncer chaque jour absence de pluie pour le lendemain aurait un taux de réussite de 70 % ! Une prévision au hasard respectant la climatologie du phénomène, c'est-à-dire annonçant la pluie dans 30 % des cas, aurait un taux de réussite de 60 %. Pas si mal ! Le taux de réussite de Météo-France est de 80 %, il y a donc une vraie réussite, mais cette valeur élevée donne une impression un peu fausse. Il serait plus précis de dire que la qualité est à mi-chemin entre les 60 % de la prévision au hasard et les 100 % de l'inaccessible prévision parfaite, mais c'est une notion plus difficile à saisir et à expliquer.

Si on s'intéressait à la même prévision de pluie-non pluie pour la capitale de l'Égypte la situation serait différente. Au Caire il y a normalement 96 % de jours sans pluie. Une prévision au hasard a alors un taux de réussite phénoménal de 92 %. Il faudra donc arriver à un taux de réussite de 96 % pour être à mi-chemin entre le hasard et la perfection et obtenir ainsi le même niveau de qualité qu'avec un taux de réussite de 80 % à Paris.

Quand au problème de biais éventuels, qui n'est heureusement gênant que pour un petit nombre d'utilisateurs, il est également masqué par la référence au taux de réussite. Il faut pour le découvrir regarder des statistiques plus complètes comptant les cas où le phénomène s'est produit sans être prévu (non détection) et ceux où il ne s'est pas produit alors qu'il était prévu (fausse alerte). À titre d'illustration on peut indiquer que sur l'année 2011, la célèbre « vigilance orange » de Météo-France a eu un taux de réussite de 86 % avec 2 % de non détection et 14 % de fausses alertes, c'est à dire un certain biais vers le pessimisme.